Predictive Analytics Using Regression Models: A Comprehensive Guide

Predictive analytics has become a cornerstone for businesses and researchers aiming to forecast future trends, behaviors, and outcomes by analyzing historical data. Among various predictive methods, regression models hold a pivotal role due to their simplicity, interpretability, and powerful ability to quantify relationships between variables. This article delves deep into predictive analytics through the lens of regression modeling, exploring how these models function, their applications, assumptions, diagnostics, and best practices to harness their full potential.

Understanding Predictive Analytics

Predictive analytics is the practice of extracting information from existing data sets to determine patterns and predict future outcomes and trends. It encompasses a variety of techniques, from machine learning algorithms to statistical models. Its applications span industries such as finance, healthcare, retail, and manufacturing, helping organizations to anticipate customer behaviors, detect fraud, optimize operations, and much more.

At the heart of many predictive analytics solutions lies regression analysis — a statistical method to model and analyze the relationships between a dependent variable and one or more independent variables.

What is Regression Analysis?

Regression analysis aims to establish a mathematical equation describing the relationship between variables. The most common form is linear regression, where the relationship between dependent variable y and independent variable(s) x is modeled as a linear function:

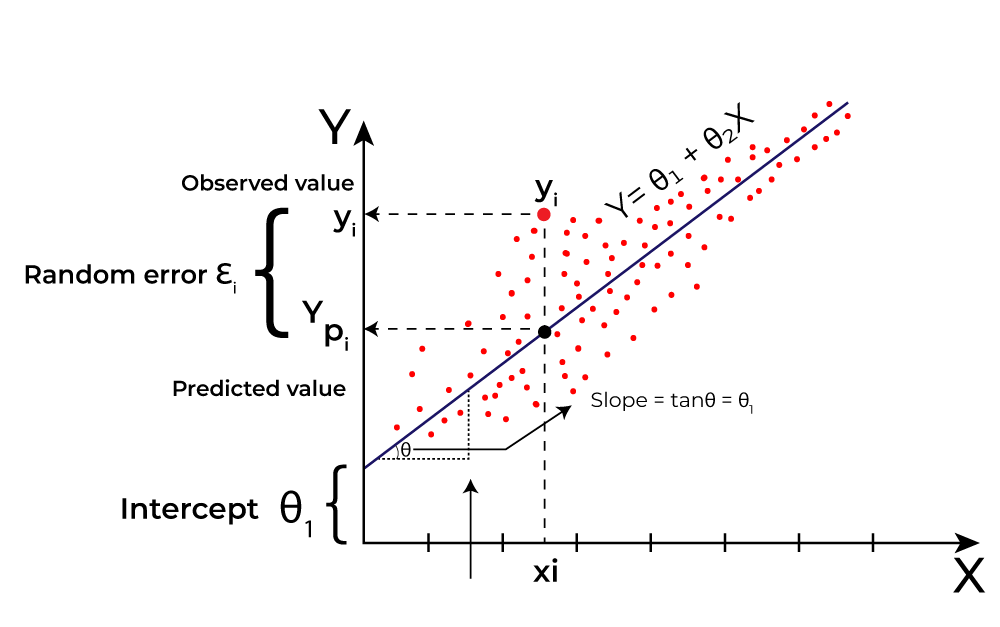
Types of Regression Models

While linear regression is the most basic, many variants exist to handle different scenarios:

• Simple Linear Regression: One predictor variable.
• Multiple Linear Regression: Multiple predictor variables.
• Polynomial Regression: Models non-linear relationships by including polynomial terms.
• Logistic Regression: For classification tasks, predicting probabilities.
• Ridge and Lasso Regression: Regularization techniques to prevent overfitting.

Why Use Regression Models in Predictive Analytics?

Regression models offer several advantages that make them indispensable in predictive analytics:

• Interpretability: Coefficients provide clear insight into how each feature impacts the target.
• Simplicity: Easy to implement and computationally efficient.
• Versatility: Suitable for a variety of data types and problems.
• Foundation: Basis for more complex models and machine learning techniques.

Building a Regression Model

Developing an effective regression model involves several key steps:

1. Define the Problem and Gather Data

Clearly articulate the business or research question. Collect relevant historical data that includes the target variable (what you want to predict) and predictor variables (features).

2. Exploratory Data Analysis (EDA)

Understand the dataset by visualizing relationships, detecting outliers, and identifying missing values. This step helps to select relevant predictors and decide on transformations.

3. Data Preprocessing

Handle missing data, encode categorical variables, and scale features if necessary. Data quality is crucial for reliable predictions.

4. Choose the Regression Model

Start with simple linear regression or multiple linear regression, and move to advanced versions if needed.

5. Train the Model

Fit the model using your training dataset. This involves estimating the coefficients \( \beta \) that minimize the difference between predicted and actual values.

6. Evaluate Model Performance

Use metrics like Mean Squared Error (MSE), Root Mean Squared Error (RMSE), R-squared (\( R^2 \)), and Adjusted \( R^2 \) to assess the model’s predictive power.

7. Validate and Tune the Model

Validate using a test dataset or cross-validation techniques. Tune hyperparameters or select features to improve performance and prevent overfitting.

8. Deploy and Monitor

Implement the model in production and continuously monitor its predictions against real outcomes, updating it when necessary.

Regression Model in Action: An Example

Imagine a retail company wants to predict monthly sales based on advertising spend, number of store visits, and discount offers. Using multiple linear regression, the company can estimate how each factor influences sales, enabling them to allocate budgets effectively.

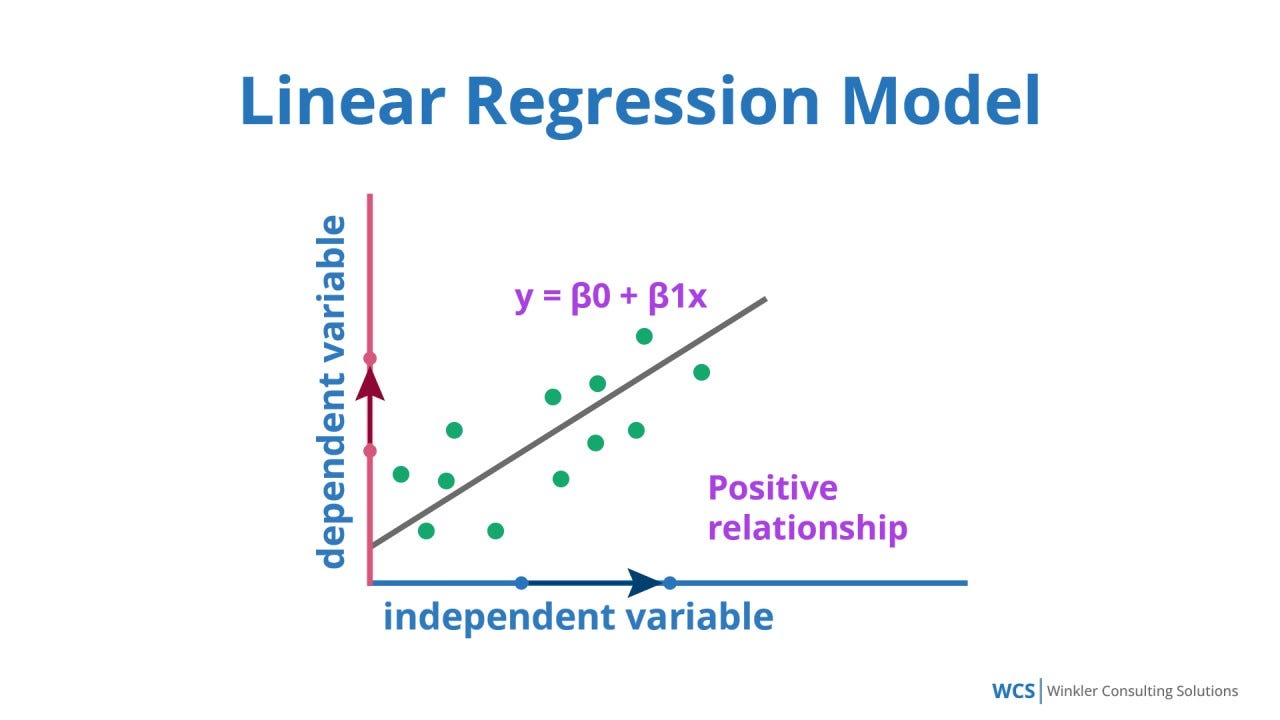
The above image illustrates the concept of fitting a regression line to data points, minimizing the distance between observed values and predicted values on the line.

Key Assumptions of Regression Models

For regression models, particularly linear regression, certain assumptions ensure valid results:

• Linearity: The relationship between predictors and target is linear.
• Independence: Observations are independent of each other.
• Homoscedasticity: Constant variance of errors across all levels of predictors.
• Normality: The errors (residuals) follow a normal distribution.
• No multicollinearity: Predictors are not highly correlated with each other.

Residual Analysis: Diagnosing the Model

Residuals are the differences between observed and predicted values. Analyzing residuals helps check if the model assumptions hold and whether the model is well-fitted.

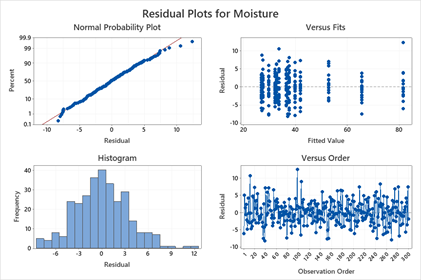
This image shows a residual plot which is used to detect non-linearity, heteroscedasticity, or outliers. Ideally, residuals should be randomly scattered around zero without any specific pattern.

Common Issues Revealed by Residual Analysis

• Patterns or curves: Suggests non-linearity in the data.
• Funnel shape: Indicates heteroscedasticity (non-constant variance).
• Outliers: Extreme residuals that can distort model accuracy.

Improving Your Regression Model

When assumptions are violated or performance is poor, consider the following:

• Transform variables: Apply log, square root, or polynomial transformations to handle non-linearity.
• Feature engineering: Create new variables that better capture relationships.
• Regularization: Use Ridge or Lasso to reduce overfitting and handle multicollinearity.
• Robust regression: Mitigate the effect of outliers.

Applications of Regression in Predictive Analytics

Regression models power predictive analytics across many sectors:

Finance

Predicting stock prices, credit scoring, risk assessment.

Healthcare

Estimating disease progression, patient readmission risks, treatment effectiveness.

Marketing

Forecasting sales, customer lifetime value, response to campaigns.

Manufacturing

Quality control, demand forecasting, predictive maintenance.

Sports

Player performance analysis, game outcome predictions.

Limitations of Regression Models

Despite their power, regression models have limitations:

• Assume linearity which may not capture complex relationships.
• Sensitive to outliers and influential data points.
• Require careful feature selection and preprocessing.
• Not ideal for categorical target variables (classification problems).

Conclusion

Regression models remain fundamental to predictive analytics by providing interpretable, actionable insights from data. While newer machine learning models gain popularity, regression’s transparency and simplicity ensure its lasting relevance. By understanding its assumptions, carefully preparing data, and conducting thorough diagnostics like residual analysis, organizations can confidently leverage regression to predict the future and drive smarter decisions.

“In the era of big data, mastering regression models unlocks the power to turn raw numbers into meaningful foresight.”

Whether you are a beginner or a seasoned analyst, refining your regression modeling skills will equip you to tackle diverse predictive challenges across industries. Start simple, experiment, validate, and continuously improve — that’s the key to predictive analytics success.